"As complexity increases, precision and meaningfulness become incompatible. While precision thrives on stable (fixed) meanings, the fuzzy meanings are unstable - they can simultaneously relate to several attractors and express specific types of meaning-generating crises. Instability of the fuzzy meanings make them flexible for interpretation and open for evolution and transformation. And these are precious qualities necessary for understanding social complexity."
Vladimir Dimitrov, Strange Attractors of Meaning, 2000
"In short, frozen components, the requirements for order, the capacity to adapt, and adaptation to the edge of chaos through natural selection may reappear at many levels in complex adapting and coadapting systems. A generalized poised state may prove to be the ultimate attractor of an evolutionary dynamic."
Stuart Kauffman, The Origins of Order, 1993, Pg. 281
Social systems are invariably complex, they do after all contain many people, doing many things and each having many values and interests. In traditional science it is usual to assume that all questions have "an answer", and it is the task of the scientist to analyse the system until they find it. Yet in complex systems such simplicity is not the case, such systems have many answers thus we must look to new techniques in order to deal with them. One of the newest findings in dynamical systems theory is the existence of what are called 'strange attractors', these are areas of state space that won't stay still, that refuse to be predictable - despite often being completely deterministic. The forms that such attractors can take and how we can regard them, in relation to social systems and behaviours, is the theme of this essay.
The following illustrative collection of strange attractors appear from nonlinear interactions of only three variables, from a formula of this form:
M( t+1 ) = a * M(t) + b * I ( t ) + c * R ( t )
I ( t+1 ) = d * I ( t ) + e * R ( t ) + f * M( t )
R ( t+1 ) = g * R (t) + h * M( t ) + j * I ( t )
If we equate M with money, I with ideas and R with resources then we have a
very simplified model of an interacting human dynamic, central to business practice.
That such a model behaves chaotically is clear, what is not so clear normally is
that the form that the 'strangeness' can take is exceedingly dependent upon the
'constants' used (a,b,c,d,e,f,g,h & j - but note that in the 'real world' there is no such thing as a 'fixed' constant, that is just a mathematical simplification). For many values of these constants (which could be quite complex functions of several parameters) we will find a fixed attractor - a single point of convergence (where M, I and R take fixed long term values), but the slightest change to any constant can force a move to any one of these strange attractors, the system 'bursts' into life (in the following pictures, all generated using J.C.Sprott's Strange Attractor program, sa256.exe, M is the x-axis, I is the y-axis, and R the z-axis colour coded into 256 shades, the 4th dimension is of course time - the sequence of 3D space points plotted). Within each of these SAs, the values cycle over the three dimensional state space, changing from iteration to iteration, moving in jerks ('quantum leaps') as well as gradually, and in some cases fragmenting into disjoint sub-attractors which (like the Lorenz) often 'escape' onto another 'wing' and later return.
Just what do these signify ? In any picture, the three axes (x, y, colour) indicate just where in the possible area of 'state space' we are located at any particular time. As time evolves (progresses) we move about the 'strange attractor' - but how far we can move is crucial here and depends upon the form of the particular 'attractor' involved. Yet these attractors are not static in themselves, they are 'unstable', they change in size, shape and number with evolution itself, thus we move between all these varied forms constantly (at least in theory - in practice, data wise, the real dynamics still eludes us).
We can identify several different forms of strange attractor within this collection (but bear in mind that in a higher number of parametric dimensions than the 3 used here other forms may appear). The names that we give to them here are simply illustrative and do not indicate any standardised academic naming of such forms. However 'dense', 'sparse' and 'tracery', as we use them, correlate with decreasing fractal dimension - compare with standard geometry where a line has dimension 1, a plane dimension 2 and a volume dimension 3 (note that the estimated fractal dimensions given below are measured using the box-counting method on the 2D image projections, if measured in 3D these would be rather higher).
In these, the area of state space involved covers most options within it, the variables can take on any combination, we can have combinations of all sorts. Note that, due to the limited number of iterations used to generate these pictures (a mere million or so...), the structure may appear 'gappy' - over time these missing areas tend to be 'filled in'. Approximate fractal dimension is 1.96.
In these there is more than one dense area which can be occupied, in the following example the M and I values of the two sub-attractors are usually very different, but at some point (around the middle values of M) we have a leap from one sub-attractor to the other (called a 'bifurcation'). Approximate fractal dimension is 1.9.
Here we have a 'hole' in the attractor, a blank centre where no solution is stable, an area of M and I values that cannot be sustained, a 'repellor'). Approximate fractal dimension is 1.93.
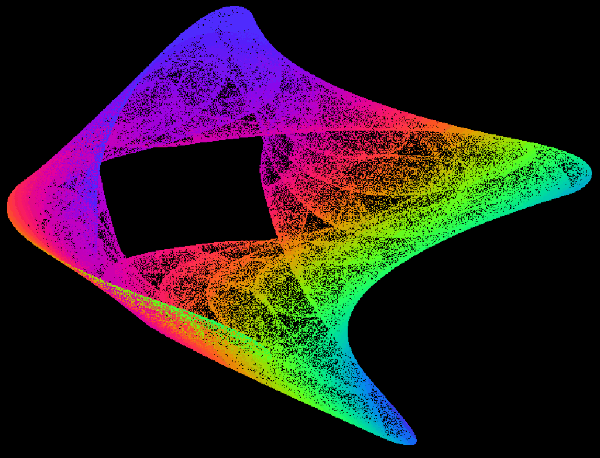
Here, like in the Lorenz attractor, we have linked wings, but note that there are several of them, not just two, so the system can flip amongst many different sub-attractors in sequence. Approximate fractal dimension is 1.86.
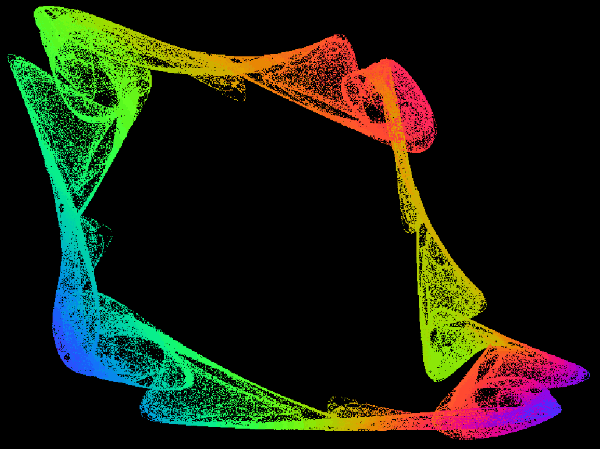
In these the areas of state space involved in the wings do not appear to be connected, we have sudden jumps between the wings and it is unclear which will be the next to occur. Approximate fractal dimension is 1.69.
Here much of state space is empty, there are many 'holes', yet we still have small wings appearing. Approximate fractal dimension is 1.63.
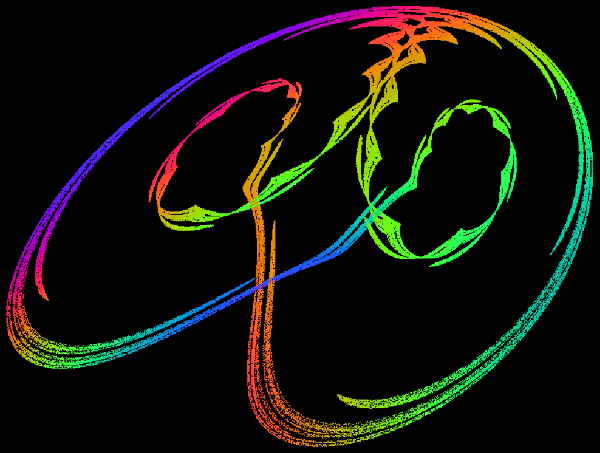
Now the possibilities seem very few, we almost have a cyclic attractor but note the complexity of its path ! Approximate fractal dimension is 1.26.
Even when we seem to have a cyclical sequence, we can find more than one, with unpredictable leaps to be expected between them. Approximate fractal dimension is 1.38.
In many cases we have combinations present of these features, and we illustrate one below, having holes, disjoint parts, wings and traceries present. Approximate fractal dimension is 1.65.
What are to make of these forms ? Do they relate to genuine social phenomena or are they just meaningless artefacts, fantasy analogies that simply confuse our understanding ? Let us look at them in turn.
Here we can see a standard social system, each variable (belief) can vary in strength over certain limits, so the net result is a set of 'values' that reflect the 'norms' of our society - go too far beyond these and you escape the 'acceptable' cultural standards and become a 'criminal' or 'enemy'.
Here we have two cultures, with incompatible viewpoints, we can exist in either one or the other, but not both. Occasionally people 'leap' across the 'divide', they change beliefs - i.e. are 'converted' from 'left' to 'right', from 'Christian' to 'Muslim' or any other standard cultural 'switch'.
In this mode there are some unacceptable possibilities, some options that are so 'outside' our worldview as to be 'unthinkable'.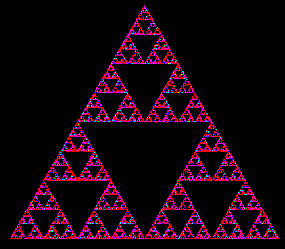
This relates to those 'holes' in our thinking suggested by Atkin's
'q-analysis'.
Here zero dimensional thinking relates to the valuation mode we call 'systemic', one dimensional to 'extrinsic' and two dimensional to 'intrinsic'. Areas of intrinsic thinking that, nethertheless, exclude some combinations of ideas have 'holes' in the matrix - forbidden combinations. We would add in also a three dimensional 'holarchic' mode which relates to the four dimensional time sequence or evolution of the whole 3D hypersystem, i.e. it considers how our thinking coevolves with that of other people, other creatures and our planet. In such a view the 'holes' take on a fractal nature - appearing everywhere and distributed over all time and space scales, in other words our thinking is generally more like the illustrated Sierpinski triangle, than what we might call rational 'joined-up writing'.
Many of our social behaviours are just routine, they follow a standardised sequence of steps, e.g. we wake, wash, dress, have breakfast, go to work, have lunch, come home, watch TV, have dinner, sleep etc. We may do slightly different things at each stage, vary our 'menus' etc., but all in all the sequence is predictable, as this attractor shows.
Breaking our daily sequence however is possible, we may do different things at weekends for example, or occasionally take holidays or get sick, and we can't always predict just when these leaps from one set of routines to another may occur or how different they will turn out to be. This attractor form can also illustrate multiple disjoint cultures, alternative lifestyles that may have little in common. From afar these relate to a set of 'vertices', systemic valuations of the 'us' or 'them' style, with no commonality accepted between them.
Some people however have more interesting lifestyles that others and may wander all over state space, lingering on any single subject for only short periods. Note however that nobody can do everything, there are many possibilities that are not explored in life's 'possibility space', many 'holes' in our knowledge (individually or collectively). This is the 'colour vision' or intrinsic valuation of a single individual, their 'lifestyle'.
Humans have a propensity to over-complicate matters. A production line may have very many steps and may need to revisit earlier stages (either for remedial work or for, say, multiple coats of 'paint' - or repeated 'adverts' !). Such sequences are however often regarded in a very rigid way and are endlessly repeated with little variation. These relate to 'edge' travel, to extrinsic valuation of each stage in the production process, measuring its 'progress'.
We can however have multiple 'products' and our production line will swap between them at irregular intervals - depending upon random 'demand'.
Given a social group of many people and 'options' however, it should be clear that at different times
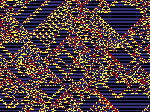we operate in all these sorts of ways, so the actual attractor we follow is more likely to be a combination type, a rather unpredictable mix of many simultaneously active social attractors (illustrated here by a 1 dimensional CA, where time runs downwards and each thread of the ever changing structure is a local attractor). This hidden form of structure relates to the 'real situation', to that 3-dimensional vision that recognises other hidden colours or possibilities, which we may need help to see (e.g. radio or x-rays) - help given (perhaps) by our metascience and holarchic valuation ideas, along with those from the complexity sciences.
We stressed initially the instability of strange attractor forms to parameter changes, so we would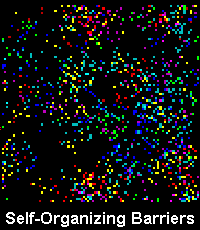 
expect that if we have multiple interacting attractors (that 'combination' type) then they will be changing each other's parameters and thus their shapes.
In fact, studies of complex dynamical systems have shown that what happens (typically) is that areas of state space that are unstable become stable, and areas that are stable simultaneously destabilise. There is thus a two way coevolution between modes moving from 'order to chaos' (barriers dissolving - the creativity of 'art'), and modes moving from 'chaos to order' (barriers forming - the rationality of 'science'), yet they swap places over time - what was 'known' becomes 'uncertain', what was 'uncertain' becomes 'known'. This finding is very relevant to social systems, and we can see this dynamic everywhere we look, most clearly perhaps in politics where oscillations between 'Right' and 'Left' occur at regular intervals, the policies of the party in power decending into chaos, whilst the opposition position stabilises and gains control of the ordering process following an election.
The net result is that the system self-organizes to attain a dynamical balance, which we call 'edge-of-chaos', where different areas of the system exist in different state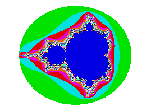s, 
so that attempts to reduce such systems to one behaviour overall are doomed to failure, we must accept that 'sets' of diverse dynamics always simultaneously exist, reminiscent of the diversity of features and attractor types present in the structure of the Mandelbrot Set.
As an example of the changes that a parameter alteration can make to attractor structure, we show below 3 attractors, based upon one varying parameter, 1.79, 1.81, 1.89 (i.e. changes of about 1%, followed by a further 4%). That such small alterations make such big differences to form (a move from 'disjoint winged', to 'excluded middle', to 'dense') needs to be read in context with the fact that in social systems it is extremely rare that any personal parameter is known to a genuine accuracy of even 5%, or has a 'standard deviation' indicating that such a narrow spread of views exists !
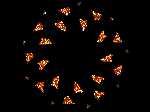
Identifying the specific strange attractors operating in society will be a difficult (if not impossible) task, especially since they are always changing ! Yet all complex dynamical systems have such attractors, society is no exception, so the general concept can help us to focus our mind upon the real dynamics of human interactions, and not get sidetracked by concepts more appropriate to more limited studies.
When we look at social situations we must be quite clear about the differences between these and those simpler systems typically studied in the physical sciences. In the latter it is usual to concentrate upon equilibrium solutions and to seek out point or cyclic attractors - labelling any situation incapable of being stated in such linear and reductionist terms as 'unscientific' and ignoring it. In such 'science' data points found outside the 'box' of predetermined expectations are actually discarded, and treated as 'experimental error' - making this a self-fulfilling and closed worldview. Physical sciences, typically, look here for one 'formula' at a time, one isolated problem at a time. Most work in the current psychological and sociological sciences tries to 'ape' this sort of technique, either discarding all the 'complexity' to look at a narrow aspect, or using statistical techniques to look at the undifferented whole - in both cases compressing the system to a single parameter (and arguing endlessly between themselves about which one to use !). But this behaviour is throwing out the 'baby' with the 'bathwater'.
Non-equilibrium systems, like society, are not comprised of single formulae, they are fractal and have diverse structure on many scales. They are composed of many autonomous elements, each operating with many different values. In the dynamics of these situations we get strange attractors, not point or cyclic ones - a society existing in such a limited attractor would be a 'dead' or 'dying' society ! In real societies we cannot predict 'exactly', solutions are nonlinear, there is a sensitivity to initial conditions, i.e. to history. There exists heterogeneity, multiple interacting dynamics, these systems are often non-deterministic - dependent upon 'random' events (like the recent tsunami). For such systems a new type of science is required, needing a new set of valuation techniques, a metascience of interconnected reality and values, which we pursue further here.