| Major Software Page | Java Applets Page |
 Alife with Dawks (DAWKS.BAS) V1.0
Alife with Dawks (DAWKS.BAS) V1.0
Order from Chaos (ORDCHAOS.BAS) V1.1
Chirikov Mapping (CHIRIKOV.BAS) V1.1
Boolean Networks (BOOLNET.BAS) V1.5
Mid Network (MIDNET.BAS) V1.1
Small Network (SMALLNET.BAS) V1.2
Variable Network (VARNET.BAS) V1.0
Attractor Maps (ATTRACT.BAS) V3.0
Asychronous Maps (ASYNC.BAS) V1.0
Phase Portrait Maps (PHASE.BAS) V1.2
Self-Organised Criticality (SOC.BAS) V1.4
Lotka-Volterra Model (LOTVOLT.BAS) V1.1
Agent Network (AGENTNET.BAS) V1.0 draft
All can be run from QBasic (supplied with Windows in the 'oldmsdos' directory) either from DOS or Windows with the command: QBASIC /RUN path\progname
e.g. QBASIC /RUN E:\COMPLEX\BOOLNET
They are supplied in .zip format.
DOWNLOAD BASIC SOURCE CODE NOW calressw.zip (57k)
They may be convertible to other dialects of BASIC on machines that support VGA (640x480 16 colour) displays.
Executable versions of the programs are also made available
for stand alone use,
DOWNLOAD EXECUTABLES NOW calresex.zip (498k)
Each program will prompt for parameters and display available options. A brief description of the function of each program follows. More detailed instructions are contained in the text files accompanying the programs.
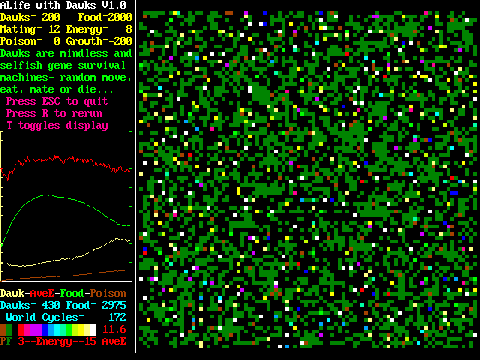
A simple Artificial Life Framework populated with
plants and an animal lifeform called the Dawk. Dawks
move randomly, eat plants and each other, mate
given the opportunity and eventually die of starvation
or poison. This simulation contains no intelligence,
no genes, no mutation. Nothing except the random
behaviour of survival machines, yet shows the
self-organizing behaviour of more complex systems.
It is designed so as to be easily modified by the
user to add more detailed features if required.
The user can enter initial Dawk and food numbers,
mating and food energies, food growth rate and
poison numbers or switch on a pollution mode
based on Dawk numbers.
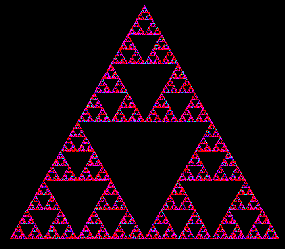
Prompts for a dimension between 3 and 100 and a move %. A start point is moved towards a randomly selected point by the specified amount. This repeats continually. That's really all there is to it ! Strangely some pretty complex patterns occur even for such a simple shift rule (including the Sierpinski Triangle). Try the 'Chaos Game' for yourself...
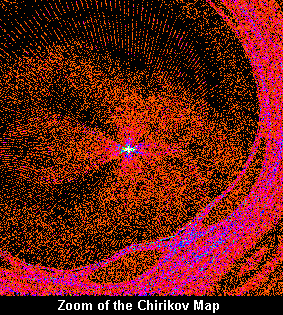
This is a chaotic map. An initially almost circular display will escape with time and cover the screen with intricate patterns and attractors. Formula is shown on the screen. User can zoom into the display and vary the parameters. Like all chaotic systems, sensitivity to initial conditions can generate large effects on the image for small modifications to the parameters.

This program is based on a matrix of 8100 logic gates, arranged in a 90 by 90 square. Each gate is two input of which there are 16 possible truth tables. The program allows the gate type to be chosen or assigned randomly from the available types. The two inputs for each are then assigned randomly to the output of another gate. Once started, each gate determines its input states and switches the output according to its logic function. This happens in parallel across all gates. The cycle is repeated as often as the user allows.
If a gate settles into a permanent on or off state (a fixed attractor) it is coloured white or black accordingly - dead states. If a gate cycles on/off at every change it is coloured blue - 50% probability of being in either state. All other gate outputs are evaluated in time to determine what percentage of the time they are on and coloured accordingly. For example a gate that only switches on once in every 5 cycles will show the 20% probability colour. Complex patterns are shown if gates enter a regular firing sequence (as part of a circuit). This display is somewhat crude but is the only way I've found of displaying what is happening without printing out some 8100 graphs ! An option to toggle the colour of probability 1 to black (same as probability 0) now makes it easier to see the structure.
You can select an individual logic gate for all the matrix, or allow the program to assign one randomly. You can also restrict the choice to a smaller number of gates -6 for example chooses from the first 6 gate types only. While running you may perturb at random the gate types to see the stability of the pattern.
The gates are listed in the rough order in which they lead to long attractors. The early gates change states easily, normally tending to give a chaotic display. The later gates tend to lock into fixed patterns with poor results. By chosing a suitable number the chaotic tendancy can be damped and perhaps order found.
result = expression1 boolean-operator expression2
boolean-operator Any of the following Boolean operators:
NOT Bit-wise complement
AND Conjunction
OR Disjunction (inclusive "or")
XOR Exclusive "or"
EQV Equivalence
IMP Implication
IF IF
Each operator returns results as indicated in the following truth
table. 1 is true ; 0 is false:
A Input B Input XOR EQV NA NB A B NOR NAND NIF IMP NIMP IF OR AND 0 1
======= ======= === === == == == = === ==== === === ==== == == === = =
0 0 0 1 1 1 0 0 1 1 0 1 0 1 0 0 0 1
0 1 1 0 1 0 0 1 0 1 1 1 0 0 1 0 0 1
1 0 1 0 0 1 1 0 0 1 0 0 1 1 1 0 0 1
1 1 0 1 0 0 1 1 0 0 0 1 0 1 1 1 0 1
----------------------------------------------------------
Rule (in Hex) 6 9 3 5 C A 1 7 2 B 4 D E 8 0 F
For this system NA and NB are NOTs whose input is just the A or B assigned input. NAND, NOR, NIMP, NIF are NOTed AND, OR, IMP and IF. EQV is NOT XOR To complete the line up we have 1 and 0 which are input independent barriers.
This is the same principle as BOOLNET except that the matrix is only 729 gates (27x27). This speeds up the cycle by a factor of 10 and allows the dynamics of changing gates and perturbations to be seen more clearly.

This is the same principle as BOOLNET except that the matrix is only
81 gates (9x9). This speeds up the cycle by a factor of 100 and allows
the dynamics of changing gates and perturbations to be seen clearly.
An additional display of the wiring is provided. Perturbations are changed
to affect the outputs only, system wiring and rules are maintained constant.
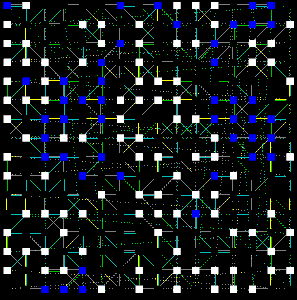
In this generalization of the Boolean Network the user can specify directly
the network size, from 3x3 to 90x90, along with connectivity distance. The
same design can then be run many times with random setups. Options to
overlay the wiring of any network, to mutate states, links or gates and to vary
the cycle speed are made available.
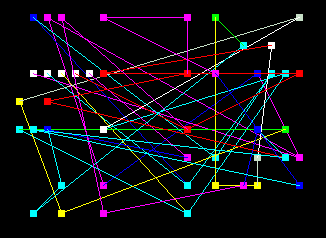
This is again the same principle as BOOLNET except that here the matrix is only 9 gates (3x3). An additional detailed display of the wiring is provided. The main feature of this program however is the ability to display the state map of the network. Even with only 9 gates we have 512 possible states of the network. These are displayed as a matrix, 32 horizontal by 16 vertical steps. Choosing the attractor option plots a box for each state entered and a line connecting them. In this way a map of the attractor basin can be plotted and the attractor cycle identified. If a state returns to itself (a point attractor) then the box is shown with a small center dot.
Options are available to start from any state, to colour cycle the attractor
and to delay the state changes for visibility. The display includes the binary
and decimal current state and last initial state. Perturbations change the state
values, and any desired output state can be specified directly. Mutation of links or gates is
allowed and automatic initial state perturbations can be selected. Update mode
is normally synchronous, but can be switched to probabilistic allowing
asynchronous and semi-synchronous modes to be simulated to investigate
transient attractors.
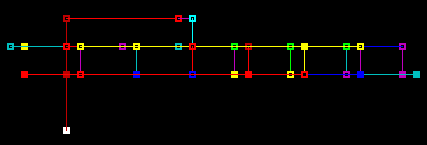
This is the same principle as ATTRACT but the program defaults here
to an asychronous update mode where only one random gate is updated
on each time step. Additionally the networks can be rerun with randomised
parameters without further parameter entry, speeding the search for interesting
configurations of transient attractors.
An addition to the Attract program, based on the same 3x3
matrix. This program analyses all 512 initial states of the
network and displays a coded picture of all the attractors
present in the network with their lengths and minimum states.
This allows the arrangement of attractors and their relationship
to gate outputs to be visualised, showing the effect of each
of the gates on the relevant attractors.
This also maps to a 90 x 90 matrix of cells, but in this case each cell
is a simple heap of units. The system generates new units one at a time
and drops them onto the matrix. Once a cell contains 4 units they then
flow from that cell to the surrounding 4 cells (horizontal and vertical)
adding one to each. Gradually the matrix fills up and the knock on effect
of filled cells then filling neighbours and so on causes avalanches or
cascades to take place over many different scales. Once such an avalanche
exceeds in size the total number of cells we have reached self-organised
criticality under my definition, loops form in the system. Past the edges
of the map the units disappear and are lost from the system. An option
is given to flow units at random rather than symmetrically.
This program shows that even for unconnected systems undergoing very
simple rules self-organisation can occur once they are pushed from
equilibrium. The time required for this to happen depends on the
distribution density but can be very quick for the drip feed option.
The program gives good feel for the time dynamics of these systems,
even on a slow processor. The behaviour shows the power law distribution
of perturbations typical in systems at the edge of chaos - too little
stress gradually builds up, too much collapses back down, the system
automatically balances itself at the critical point or phase boundary.
Somewhat different, this simply graphs in time the co-evolution of two
populations following the equations designed by Lotka and Volterra.
A population growth of 10 means an increase of 10% a cycle, but it will
also die out at some rate eg 0.1 allows 0.1% to die each cycle. The coupling
is the effect on population A of B, and on B of A.
The standard model assumes A is the prey, B the predator. So the coupling
for A is negative (B eats it!) and reduces the population. Similarly the
coupling for B is positive (A provides food) and B will increase. Depending
upon parameters the system can settle, oscillate or go chaotic. The default
looks to cycle evenly but does in fact become wildly erratic in time.
Alternative models are possible with the same formulae. Both couplings can be made
negative - simulating an arms race, or both can be positive - simulating
co-operation, mutual benefit or symbiosis.
A fully functional version is currently under development, but many options are
currently available as an ongoing preview in four types:
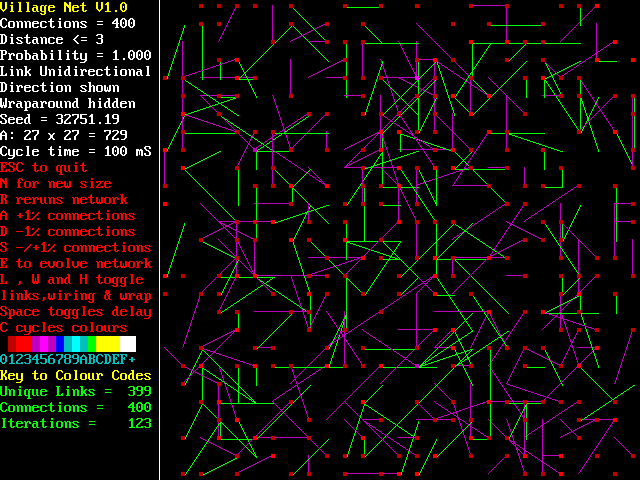
This simulates a set of agents connected with a specified number of links in either symmetrical or small-world arrangements. The network is generated randomly to model many stochastic 'encounter'
scenarios. The links can be 1-way or 2-way, they can be dynamically added, deleted or rearranged. Connections can prove to be multiple on any link (strength related, as in neural nets)
or single. Displays of the layout by link strength or distance are possible, links going from one side of the (wraparounded) display can be shown or hidden (they are dotted if they exceed the specified distance). Wiring can be displayed or hidden. Initial display shows the strength of the links and nodes in terms of connections. The node display dynamics changes as the network is asked to evolve (in one of four current modes).
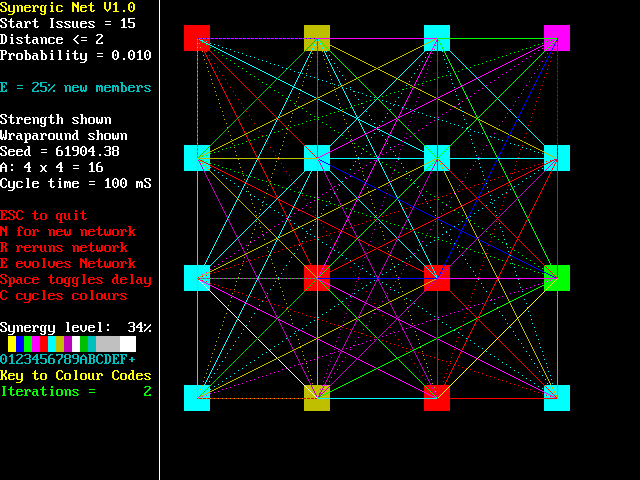
Synergy relates to the emergent benefits of working together, i.e. cooperation, essential we would say to any sustainable society. This model simulates a 4 by 4 fully connected bidirectional matrix (16 agents, 120 links). Each agent is initialised with a random 15 bit number. The processing currently consists of scanning all links and comparing, bit by bit, the two agents involved. If they agree (i.e. are synergic) no action is taken. If a bit
mismatches then probabilistically the bit is set to match in both agents (simulating compromise
or agreement). This repeats until all agents are synergic with all the others. As the
processing proceeds the links are coloured as to how synergic each pair
of agents currently are, and the nodes as to how synergic each is to all
other agents (averaged out). The percentage synergy is dynamically shown
and when this reaches 100% the number of iterations to reach synergy is shown
for reference and 'Auto Member Swap' is switched on. This changes a single
random agent to a new randomized one every 50 cycles - simulating one team
member leaving and being replaced by someone with different views.
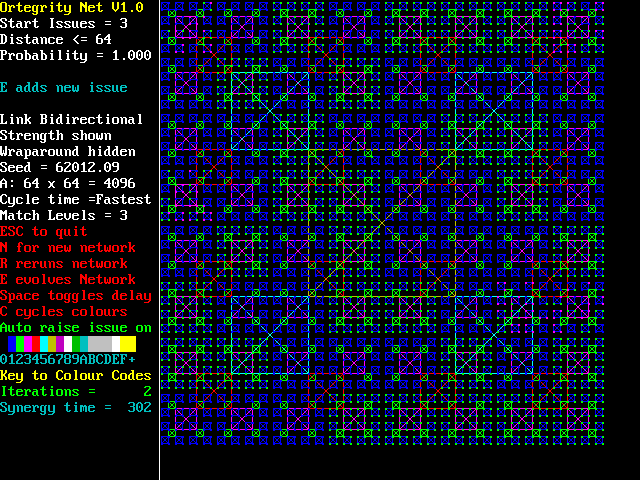
Ortegrity (or Organizational Tensegrity) is an hierarchical synergic method of
organization suggested as fundamental in nature by Timothy Wilken of SynEarth,
for more technical details on both OT and Synergy see his detailed description. In this model the base matrices are 2 x 2 (4 agents, 6 connections). This is Level 1. One of these agents then forms a part of a Level 2, 2 x 2 matrix - which links 4 base matrices. This is repeated at
successively higher levels, linking 16, 64, 256 and 1024 to arrive at an
overall 4096 interconnected agents (8190 connections). The number of contentious
issues is specified. Each matrix then seeks to arrive at synergy in turn (6 steps at a time).
Three methods are currently available. The number of adjustments
to agent states is dynamically shown and when this reaches zero the number of
iterations to reach synergy is shown for reference and 'Auto Issue Generation'
is switched on. This initiates a single random agent every 20 cycles as supporting a new random issue.
This simulates a selectable number of cults randomly initialised. Each cycle, the agents randomly look to another agent and probabilistically adopt their cult. The network evolves in
time, looking rather like the 'Game of Life" (which I suppose it is !), often settling
down to a single dominant cult (due to positive feedback) - less likely if the probability of 'conversion' (agent susceptibility) is set low or is made population or threshold dependent (adding negative feedback). These 'cults' could be religions, fashions, fads, enterprises or any form of competing social 'beliefs'. On a different level this can also be regarded as a simulation of how different ideas compete for dominance in the brain (e.g. Calvin's 'Darwin Machine"). The number of existing cultures is shown dynamically, as is the time for all variety to die out. If this happens 'Auto Deviancy' is switched in which a single random new 'deviant' is introduced to a random agent every 10 cycles to see if this new cult 'catches on'.
These programs are provided free for any non-commercial use.
I can't guarantee warranty or support of any sort, but if any bugs are
found (and there are always some...) please EMail details to me and I'll
try to correct.
DOWNLOAD BASIC SOURCE CODE NOW calressw.zip (57k)
ASYCHRONOUS MAPS V1.0
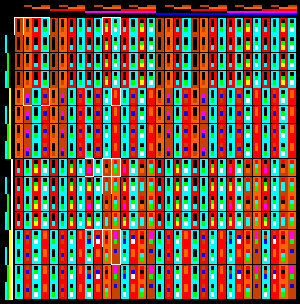
PHASE PORTRAIT MAPS V1.2
SELF-ORGANISED CRITICALITY V1.4

LOTKA-VOLTERRA MODEL V1.1
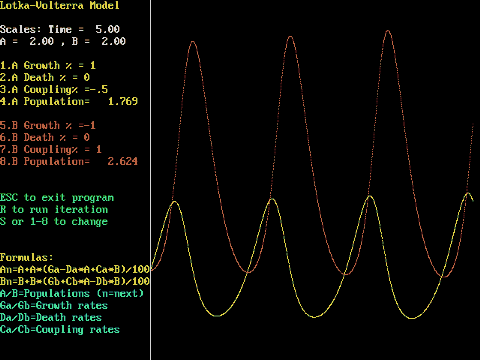 Each equation has a population A or B, a growth rate Ga or Gb, a death
rate Da or Db and a coupling rate Ca or Cb.
Each equation has a population A or B, a growth rate Ga or Gb, a death
rate Da or Db and a coupling rate Ca or Cb.
Under development...
AGENT NETWORK V1.0
General Net
Synergic Net
Ortegrity Net
Culture Net

DOWNLOAD EXECUTABLES NOW calresex.zip (498k)
Chris Lucas
Complexity and Artificial Life Research, New Mills, Derbyshire, U.K.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Page Version 4.83 June 2012 (original August 1997)