"Why is geometry often described as 'cold' and 'dry' ?
One reason lies in its inability to describe the shape of
a cloud, a mountain, a coastline, a tree..."Benoit Mandelbrot, The Fractal Geometry of Nature, 1977, Ch 1
"A man may love a paradox without either losing his wit or his honesty."Ralph Waldo Emerson, Uncollected Prose, 1841
A galaxy, a lung, a coastline, a tree
A figure that has more than two and less than three dimensions
A figure with an infinite perimeter and zero area
A solid that contains only two dimensions
A figure which changes its shape the closer you look at it
A figure that looks the same at any scale ?
All of these are related to the same thing, the magic of fractals !
Of course they do you say ! Ah, but they know roughly the area of the country so they must, by Euclid, know the minimum boundary surely, an equivalent circle ? Yes, but the actual boundary is almost infinite ! To see this, go in your mind to the seaside with a metre rule and measure a section of rock. You will skip over a few crevices will you not ? Now use a kilometre ruler instead - this skips over a lot more resulting in a different, lower reading. Take now a 1 cm measurement, this will go around most irregularities and give a much bigger total. So, the length is variable isn't it ? But not infinite surely ?
Move up the coast and you find a river. What do you measure now ? Well, just continue up the left bank until you re-emerge on the right, the coastline must be continuous ! But now you are following all the tributaries and streams and rivulets and....you will never appear on the other side I think ! If you do, take an micron sized measuring stick and try again, by the time you have measured every soil particle you will have effectively have used infinite time. Britain thus has an coastline approaching infinity but a finite area. A 2 dimensional paradox.
Now take a tree and measure its volume (easy, just dunk it in a big bath and see how much water overflows, like Archimedes would). But what is its surface area ? Yes, that's right it's nearly infinite again (don't forget to measure down every pore or stomata in every leaf...). A 3 dimensional paradox now !
How many dimensions did I say ? Two ? Three ? Neither are right, both items have
what is called 'Fractal Dimension' - a fractional number. Ignoring technicalities,
this is a measure of how irregular an object is. A Koch snowflake (a triangle, with other
third size triangles stuck midway on each side, and so ad infinitum - illustrated) has for example a fractal dimension of 1.26. In the extreme cases we have seen the dimension become
one more than we would expect, a single dimensional line becomes two dimensional,
a two dimensional surface becomes three. I'll leave to your imagination a 3 dimensional
fractal in 4 dimensions !
Can we go the other way, reducing a three dimensional object to two ? Yes we can. Take a pyramid and drill a hole in it. We increase the surface area and reduce the volume. Keep drilling smaller holes in what is left until you run out of material, you now have a solid without any volume, made up only of edges. The formal version of this is called the Sierpinski gasket in three dimensions, but has a fractal dimension of only two !
While measuring the coast with the different ruler sizes something may have struck you. The shape of the coast at 1km scale is the same as at 1m scales, and again the same at 1cm scale. Think of Africa from space, an island on a map, a rock pool beneath your feet. The shape of the coastline always appears the same, equally jagged. This is a feature of fractal systems which we call 'Self-Similarity'. We cannot tell just by looking at a system what scale it really is. Yet every view is slightly different, the objects are identical in form but also not identical in detail ! Why is this ?
To see let us look at something quite different. Many people know that you can find the roots of an equation involving squares of x by using a simple formula, and it gives two values. Generalising, we can expect n roots for an equation of x to the power of n. How do we solve these bigger equations ? Often Newton's method is used, this is an iterative solution and gives a better approximation by putting the last answer back into the equation, repeating until the answer doesn't change - that being a solution. For other solutions we try different starting values and, if lucky, the formula will converge to an alternative solution. Luck ? This is precise mathematics isn't it ? Not quite, it is another fractal !
The boundary between the range of values converging on one root and those converging on another
is a fractal curve. If we guess a value close to this boundary we cannot be sure which root it will converge towards. It makes no difference if we magnify a graph of value versus root, the irregularity and unpredictability of the boundary is still there, big as ever (as illustrated in this plot of x6). It is this boundary between part of a system moving in one direction and part moving in another which is at the heart of fractals.
The sensitivity to initial conditions is a feature of the phenomena we call 'Chaos', and a fractal boundary is usually a manifestation of a chaotic state of the system. Let us now take the most famous fractal image of all time, that of the Mandelbrot set, what does this show us ?
Well, any two dimensional system can be related to x and y co-ordinates (just two numbers specifying the position in vertical and horizontal directions).
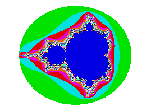If we pick two such numbers at random and iterate them in the same way we did for the Newton solutions, but using the Mandel formula z = z2 + c (where both z & c are complex, i.e. two dimensional, numbers), we can see what solutions arise. The result may go to zero (or stay bounded at least), or grow continually (like repeatedly squaring 2) towards infinity. If it stays bounded let's colour the x/y point on our picture blue. If it grows, let us colour it according to how quickly it exceeds, say 2. If we do this for every x/y point then we have the normal picture for a Mandelbrot set (right). The fractal boundary is the edge between the central blue 'sea' and the rest of the picture. If we zoom in to this edge we obtain all the wondrously detailed fractal images that you may have already seen. The attractors we find are determined by their position in the sea, the centre cardioid is a point attractor, the smaller one to the left is a 2-cycle, next to that a 4-cycle is found, the cardioids at the top and bottom (called bulbs) usually have odd number cycles. There is a infinite structure (including strange attractors) hidden deep within this sea - full of 'sea horses', 'elephants' and 'rabbits', if you choose to explore.
The formula for the Mandelbrot set is only one of a vast number of possible formulae that can
generate fractal boundaries, in fact there are more formulae that are fractal at some values than those that are well behaved. Even magnetic phase transitions have their own share of fractals, and lo and behold if we zoom into such a magnetic fractal we find, lurking in the depths, our old friend, the Mandelbrot set !
A strange world indeed, but it is our world...