"Lo ! thy dread empire Chaos ! is restored:
Light dies before thy uncreating word;
Thy hand, great Anarch ! lets the curtain fall,
And universal darkness buries all."Alexander Pope, The Dunciad, 1728-1743, bk. IV
"The ultimate meaning of the systems approach, therefore, lies in the creation of a theory of deception and in a fuller understanding of the ways in which the human being can be deceived about his world"
C. West Churchman, The Systems Approach, 1968
The terms "linear" and "nonlinear" are often made synonymous mathematically with simple and difficult. Linear is a property of straight lines, of simple proportions, of predictability and good behaviour. Nonlinear on the other hand applies to systems that do unpredictable things, that cannot be solved exactly and need to be approximated, the one-offs that don't fit the expected pattern.
So now that we understand these terms, what things are nonlinear exactly ?
Answer - almost everything !
Nearly all of the mathematics and science with which we are familiar is presented in a linear form - that is, the output of the equation varies in direct proportion to the input y = f(x). This seems very natural to us, and we often take for granted that the world works like this - a ball hit twice as hard will go twice as fast; a hole twice as big will leak twice as much water. If this were not true then we would have great difficulty in predicting anything wouldn't we ?
It comes as a surprise to many people that the natural state of affairs in the world is non-linear. Linearity is merely an approximation. Let us demonstrate this by a simple thought experiment. One of the most frequent demonstrations of Newtonian linear dynamics is the billiard ball model of atoms. Conservation of momentum and energy allow us to predict exactly the trajectories of atoms moving in straight lines. A neat trick on the college blackboard, but does it work in real life ? Unfortunately the answer is a qualified no.
Let us take the air itself. We will assume that it is at a constant temperature and pressure and comprises atoms that collide elastically (no energy lost as heat). For how long could we predict the trajectories of the molecules (given an ideal computer) ? The answer is almost no time at all, a few collisions only, a tiny fraction of a second. The system is nonlinear, as are all real systems. This also means that they are irreversible, contrary to conventional assumptions.
Why ? Well, the billiard ball model, like most models, is a simplified treatment. It ignores gravity for instance. Atoms are subject to it in the same way as are planets. It can be shown that the gravitational attraction of a single electron, at the edge of the known universe (10 billion light years away), is sufficient to deflect an oxygen molecule in the air on earth by enough to miss a predicted destination molecule within about 50 collisions, around one hundred millionth of a second !

This phenomena is known as sensitivity to initial conditions, or the Butterfly Effect. It arises because the errors that accumulate from each collision do not simply add (as linear analyses assume), but increase exponentially and this geometric progression rapidly diverges any initial state to one that is unpredictably far from the estimate. This behaviour is responsible for what we call Chaos, a term that has a technical meaning but is roughly equivalent to the common notion of future randomness, except that the states in which the system may be found are often restricted and known in total - we just don't know which one it will be in at any future time. The system is unstable, a small change leads to a massive reaction...
Each molecule is acted upon by every object in the universe - an infinite sum of terms is thus necessary for an exact model. If we take the totality of the interactions between molecules (non-stationary - hence irreversibility, the return path would experience different forces) we can see that the normal linear treatment (discarding most terms) is woefully inadequate, so why does it ever work ? Well, we have four factors at play here.
Firstly, we do not generally require to predict the trajectories of the individual components of gasses (and similar multi-agent systems), instead we adopt a statistical treatment - we smooth out and average the uncertainties (sum-over in the parlance). We can do this because even a small system contains vast numbers of particles. If we are only interested in overall effects, then the minor short term individual deviations will, on average, cancel out.
Secondly for larger one-off objects we do not need to predict over long time periods. Thirdly, usually in these cases we need take no account of any collisions with systems of the same order of size. Planetary predictions cover a short cosmic time scale relative to the frequency of collision with similar sized asteroids, and the gravitational effects of distant planets or collisions with smaller objects (meteors) are assumed negligible over these short periods - these terms can be neglected, in some circumstances...
But what about longer periods ? It is true to say that in that case our predictions are known to break down - the Earth's orbit is chaotic over a mere 5 million years, all systems of 3 or more bodies may exhibit such chaotic dynamics. We cannot predict forward or backwards for very long in astronomical terms, so extrapolations to the beginning or end of time would be little more than guesswork - apart, perhaps, for our final factor.
That fourth reason is most interesting, and concerns the constraints on the system. Most familiar systems do not have the freedom to move that we attribute to ideal gasses (on which traditional dynamics are based). A planet is held together by gravity, a chemical substance by molecular bonds. Structure implies the presence of forces acting to prevent the system disintegrating - the system does not have available the maximum degrees of freedom.
If a molecule in a solid is attracted away from its position, then the forces from neighbouring molecules act to restore that position - there is a negative feedback effect, the displacement is no longer linear. Any time that we have a system that has limits, minimum or maximum settings, then we have a nonlinear system. Populations of animals are limited by food, space or predators; trignometrical functions are limited, elastic stretching is limited, pendulum swings are limited. All aspects of our perceived reality are, at root, nonlinear - none are completely unrestrained. The formula we now need is x = f(x), the output is a function of itself. Positive feedback, hence we have potential instability.
Let us compare the two formulae, y = f(x) and x = f(x).
Take first the equation y = x * n.
Suppose n = 2, then plotting for x = 1, 2, 3 we have y = 2, 4, 6 - a straight line, of slope n and linearity.
Now for x = x * n. Again for n = 2, starting with x = 1 we have x = 2, 4, 8 - an exponential progression
towards infinity, if n = 1 we have 1, 1, 1 - stagnation and for n = 0.5 we have 0.5, 0.25, 0.125 a progression
towards zero. Three very different behaviours from the same formula, dependent upon the constant. If
we assume that it is one then anything even slightly more will take us eventually to infinity, any less to zero
- our 'Butterfly Effect', sensitivity to initial conditions appears even for such a trivial formula.
In real life we will usually have many coupled variables, so in practice x,y,z,... = f(x,y,z,...) - a matrix of inter-dependencies. The 'constants' in nature (say 'reproduction rate') are usually nothing of the sort, merely our assumptions. The behaviours we then predict are highly dependent upon what we have chosen to assume initially - our axioms !
Is it possible to control these nonlinear systems ? For us to do this we need to understand under what circumstances they become chaotic. To some extent we have already tried to do this with our linear approximations, effectively we have only operated our predictions in regions where the system behaves almost linearly. This means restricting the parameters of the system to areas that do not possess the sensitivity to initial conditions or studying only simplified aspects of systems.
Unfortunately, when we deal with complex systems of the type of interest to researchers in our fields, that is rarely an option. Strong feedback (positive as well as negative) and many interactions mean that chaotic behaviour is potentially always just around the corner, disastrously if unsuspected (say in an aircraft control system). We need to find a way of controlling chaos, to understand what may happen long term. Luckily we have some tools at our disposal.
Chaotic systems are not totally random, they usually have well defined limits (trajectories in phase space), so to a first approximation we can determine limits for the system. If we are happy to use statistical analysis then this may suffice, we can (like in quantum mechanics) assign a probability to the system being in a particular state (actually within a small region of phase space).
We have seen that small perturbations can send chaotic systems into very different states, so a further technique relates to this. We can arrange to perturb the system in a controlled way to keep it in the region of behaviour that we need. A similar idea is to add additional constraints to change the global dynamics until all the states available to the system fall within permitted boundaries.
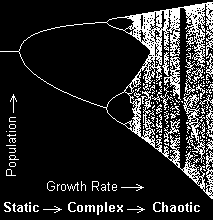
If we plot the behaviour of many nonlinear formulae against changes in parameters we see an interesting phenomenon. At certain values of a control parameter the system changes phase - it moves from a regular behaviour to a chaotic one. The first stage in this is what is known as a Bifurcation, the system splits from one state to two possible states. As the parameter changes further, additional splits take place at intervals dependent upon a constant, the Feigenbaum number (4.669...), giving more complex limit cycles progressively until the system enters a chaotic state. We can therefore determine the parameter ranges that lead to the behaviour we desire, and try to constrain the system accordingly.
What about systems whose formulae are unknown ? Here we have a problem. If we can only sample a few states of a system we cannot with any certainty determine its limits. It is here that computer simulations come to the fore, allowing us to investigate the general behaviour of nonlinear systems and to try to understand and categorise them. If we are able to assign to natural systems an appropriate general behaviour, then we may be well on the way to controlling that most difficult and unpredictable of chaotic human problems - our social interactions.