"Daring ideas are like chessmen moved forward;
they may be beaten, but they may start a winning game."Johann Wolfgang von Goethe (1749-1832)
"What a man believes may be ascertained, not from his creed,
but from the assumptions on which he habitually acts."George Bernard Shaw (1856-1950)
Philosophy is essentially about the questioning of assumptions, those axioms that form the starting point for any mathematical or scientific perspective. The various fields that comprise the complexity sciences utilise a set of axioms that differs in many ways from those used in conventional science. Here we will introduce our take on the ideas that comprise this new viewpoint or 'paradigm' and contrast them with traditional views, in a way that emphasises the value of this new thinking. We will also try to pull together our series of thematic introductions into an integrated whole. The complexity viewpoint is not however restricted to scientific areas and can usefully be employed in considering many personal and social situations where complex interactions and difficult decisions need to be evaluated.
Many of our philosophical ideas are not made explicit in our education, but develop unconsciously as we grow and as we absorb our social and intellectual environments. We have a considerable bias towards simplification and in many situations will reduce a complex multidimensional issue to a one-dimensional form more conducive to an either/or decision. Complexity thinking looks to recognising the situations where this is invalid and to providing an alternative form of treatment that can better deal with these problems - the philosophy of complexity. This combines, in our view, three strands of thought, systems thinking (incorporating cybernetics) which relates to non-specific systems, organic thinking (including evolution) relating to non-static systems, and connectionist thinking (attractor based) relating to non-reductionism. Let us consider each in turn. See the glossary for any unfamiliar terms.
The term 'system' is used in many ways, for example in solar system, social system, ecosystem, hi-fi system and so on. All these uses relate to groups of related entities. Systems thinking is an interdisciplinary field that looks to find common properties across all these forms of organization, and therefore studies generalised or abstract systems, rather than the more conventional specific forms. Normally we associate the idea with cybernetics, a type of system that incorporates feedback, causal loops that force nonlinear behaviours, and which develops homeostasis or constancy in system space. These sort of systems are self-contained and self-regulatory, we cannot look at the parts in isolation but must consider the overall (holistic) purpose of the system. This relates to emergence, the generation of new higher level system properties that contain functions that do not exist in any of the parts.
Organic systems have a metabolism, they are both self-producing (they manufacture their own parts, unlike artificial systems) and self-maintaining (self-repair is possible).
We can illustrate an organic system by the following biological picture:
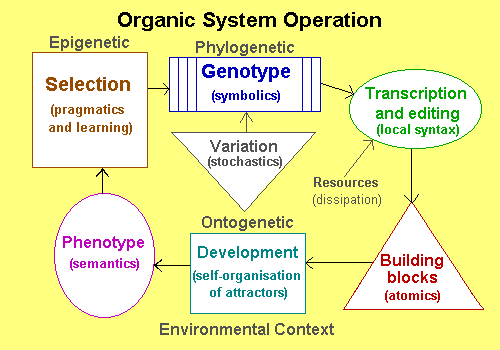
They are often called autopoietic systems. They are responsive to their environment, but unlike general cybernetic systems are also adaptive, discovering new behaviours over time - they are innovative. This relates to associative learning and over a longer evolutionary period to genetic algorithms where coevolution amongst large populations by natural selection plays a part. In these systems part interactions are often stochastic or indeterminate, and control is distributed not centralised, again differing from more conventional systems.
The idea of connectionism is derived from artificial neural networks in cognitive science, where inter-unit wiring is both explicit and brain like, and employs a distributed data structure. But we can generalise this idea also to cases where the connections use adjacency (cellular automata), logic (boolean networks), information (cas) and sensors (artificial life). These systems all and that is one of the defining features of connectionist systems, the connections allow information to communicate across the system and the system closure (feedback loops) then causes attractors to form. How the connectivity is arranged is crucial to the style of system obtained since the system is defined by the connections and not by the parts (as in reductionism). This permits static, chaotic and organized modes of operation, along with more complex dynamical systems exhibiting mixtures of these modes.
Putting these three strands together we arrive at our prototype complex system (the divisions outlined above are somewhat arbitrary and many ideas appear historically in more than one of these viewpoints, we have not attempted to be definitive here). The effects of the various features mentioned creates what we call a Type 4 self-organizing complex system, which is based upon the following assumptions that differ from those adopted in conventional scientific work (note however that different complexity researchers may include different sets of axioms, and may also define them differently - this is still a very tentative and provisional list):
Complex systems are generally composed of independent or autonomous agents (not the identical parts often assumed in science). All of these agents are regarded as equally valuable in the operation of the system (there is initially an anarchic power symmetry). No executive or directing node exists (by design) in these systems, which gives an absence of central or external control. Therefore any control structure or leadership (a power asymmetry) must emerge by self-organisation and cannot be imposed.
Complex system outputs are not proportional to their inputs. This means that reductionist superposition - the idea that F(x+y) = F(x) + F(y) and that F(ax) = aF(x) - does not hold in this nonlinear science. Thus taking the properties of each part and adding them will not give a valid solution to overall fitness - the whole is different than the sum of the parts. Mutual interference (epistasis) between the parts requires that we analyse the system in an holistic way.
The system properties are thus not describable in terms of their parts, they are emergent or higher level functions of the system. These functions or properties will not even be describable using the language applicable to the parts only, and are what have been called 'Meta-System Transitions' or evolutionary transitions. They comprise forms of synergy or cooperation that go beyond the simple ideas of aggregation used in reductionist science (and disprove the Laplacean deterministic fallacy that claimed that all system behaviour is predictable from total part data).
Along with the traditional form of upward causation (the parts creating the whole) we have in complex systems a downward form also. This means that the existence and properties of the parts themselves are affected by the emergent properties (or higher level systemic features) of the whole, which form constraints or boundary conditions on the freedom of the constituents. For example, we, as humans, determine (by our actions) the fate of our cells just as much as their function determines us, and this two way structural interplay is common in complex systems.
Self-organization relates to the presence in the system of dynamical attractors. Each attractor will occupy a relatively small area of overall state space. The system will thus be expected to contain multiple alternative attractors (areas of stable operation - concurrent options or 'choices'), giving several different possible behaviours for the same system. Which actually occurs will depend upon both the initial configuration and the subsequent perturbations and transients (the system history). This compares to conventional science where history is discarded.
The distribution of choices or optima around state space can be modelled by the concept of a fitness landscape. Here the height of the hills relates to how good the option is (this landscape is contextually dependent). Unlike conventional ideas, we are looking here at all the possibilities open to the system and not just the current actuality.
The parts are regarded as evolving in conjunction with each other in order to fit into a wider system environment, thus fitness must be measured in contextual terms as a dynamic fitness for the current niche, and not in relation to any imposed static function. The part structure will correlate to an external environment (giving a contextual fitness by structural coupling). This dependence upon environment contrasts with the isolated treatments of conventional science.
These systems operate far from equilibrium since they are dissipative (i.e. they take energy from their environment to maintain the far-from-equilibrium position). Energy flows will drive the system away from an equilibrium position and establish semi-stable modes as dynamic attractors. This relates to the metabolic self-sustaining activity which in living systems is usually called autopoiesis. These active systems reduce local entropy whilst exporting it to the environment, unlike conventional passive systems.
Complex systems contain structures in space and time (thus are heterogeneous rather than the homogeneous assumption from conventional science). Their part freedoms will allow varying associations or movement, permitting clumping and changes over time, thus initially homogenous systems will develop self-organizing structures dynamically (therefore order increases over time rather than decreasing as expected in conventional thought).
These parts are non-equivalent (thus each can obey different rules or local laws - rather than all behaving the same under the global laws of conventional science). Each part evolves separately, giving a diversity in rule or task space. The mix of rules (learning) that occurs will depend upon the system's overall contextual coevolution.
Feedback processes lead to phase changes, sudden jumps in system properties. These 'edge of chaos' states are critical points in connectivity terms and the system is maintained at the phase boundary by its self-organising dynamics - very different than the either/or phases of conventional systems. At this point a power law distribution of properties and perturbations occurs in both space and time. These systems exhibit the self-similarity of fractals, but in a statistical rather than an exact way.
In such interacting systems a chaotic sensitivity to initial conditions can occur (the butterfly effect). Trajectories differ, some show this divergence in state space from nominally similar inputs, others show convergence to an attractor. This is a feature of the mix of attractors typically present at that point (unlike the single attractor of equilibrium dynamics).
Over the long term stepped evolution or catastrophes will exist (similar to punctuated equilibria). Sudden swaps between attractors become possible as the system parameters approach the boundaries of the attractors. Evolution thus is expected to operate in steps rather than gradually, with the wild swings in coevolutionary balance often associated with perturbations to ecosystems being seen. The steady state models of conventional science are rather different.
Random internal changes (mutations) or innovations typically occur in these systems. New configurations become possible due to part creation, destruction or modification. This relates to changes to the structure of state space, which must be regarded as dynamic, not static and does not conserve world lines as in conventional science, here they may bifurcate and merge over time.
Usually these systems have an ability to clone identical or edited copies (growth). Even social systems can replicate to create additional systems (e.g. organizations or franchises). Copying errors (including mutations, recombination or insertion) permit new system structures to become available, allowing open ended evolution and self-generation (autocatalysis). This discards the fixed-in-time assumption of most science.
Parts can change their associations or connectivity freely - either randomly or by evolved learning procedures. Thus the system can be regarded as redesigning itself over time, as far as proves necessary to maintain or change function within its operating context. These internally generated system changes are missing from most scientific viewpoints, which assume instructional changes.
The meaning of the system's interface with the environment is not initially specified and this must evolve. This requires that semantic values or communications are created dynamically (or constructed) by the system as a result of environmental interaction and are not simply a direct reflection (mapping) of the external world (as usually assumed). This is a contextual (constructivist) semantics rather than an absolute view of external truth.
The overall system function is thus not initially known, but is created by coevolutionary methods. This relates to combinations of the emergent values creating an implicit theory of operation, in which sharp dualist classifications are unavailable and probabilistic matching between system and environment must suffice. This is a fuzzy functionality very different to standard bivalent logic.
We can summarise the structure of complex systems in an overall heterarchical view where successively higher levels show a many to many (N:M) structure, rather than the top down (1:N) tree structure common to conventional thought.
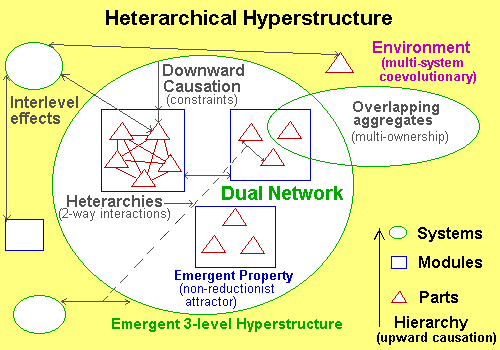
Here the 'part' interactions will create emergent 'modules' with new properties. These modules themselves interact as parts at an higher level and this process leads to the creation of an emergent hierarchical 'system' (the upward causation). The components at each level also connect horizontally to form an heterarchy - an evolving web like network of associations which generates the autocatalysis or self-production aspect of the system. Additionally systems can have overlapping members at each level (e.g. individuals can belong to many social groups, molecules to many substances, a situation to many models and a model to many situations). These groups of interlaced networks are coevolutionarily constrained by downward causalities.
This extended design we call here an heterarchical hyperstructure (to reflect the flexible inter-relationships between levels typical of human systems). We could also call this three dimensional structure a CAS cube (intrasystem, interlevel, intersystem) or a triple network. Natural hyperstructures typically will have thousands of components and connections per system, rather than the few shown here for illustration, and generally therefore complex systems are very high dimensional. Given that a metasystem (the set of systems) has such a set of structures, then the overall fitness of any part will relate to the interdependent properties at all levels, in other words to the full contextual environment.
Despite the apparent differences between complexity thinking and conventional science, what we have here is a superset concept of science and life, which includes many areas left out of conventional treatments. The conventional positions can be restored by forcing global constraints (axioms) back onto system space, thus reducing the scope of the systems studied towards either the static (Newtonian) or chaotic (statistical) ends of the scientific continuum. These techniques can be used in other areas also, for example in production systems which mix expert system and cognitive learning techniques to form classifiers.
Possible applications of complexity thought pervade all our human areas, and in this respect we are considering agents that are aware and goal driven in some sense. This awareness has arisen biologically, and this developmental aspect of complexity brings in evolutionary psychology and L-systems. The main 'aware' characteristics of the type 4 complex systems often studied we consider to be:
Breaking away from the constraints of old-style scientific axioms (which nethertheless remain valid within their limited domains) allows us to explore an organic world that until now has been difficult to understand in overall terms. In such high-dimensional (multivalued) systems reductionist thinking proves inadequate, isolated single dimensional results do not predict real system behaviours. The coevolutionary or epistatic nature of interrelated systems requires us to take a contextual approach, studying the dynamics of interactions rather than the static makeup of parts studied in more conventional science.
Contextual approaches recognise that systems do not exist in isolation, but are defined only in conjunction with other systems (including that of the observer). This coevolutionary nature of multiple systems brings us to an ecosystem viewpoint and allows us to understand the irregular changes over time that characterise such systems. This viewpoint is not emphasised in the assumptions of our conventional sciences, which are based on static snapshots of what are non-static systems. In complex systems solutions are always compromises, there is no single answer. What we must do instead is to compare alternative answers or options in state space, using a plurality of techniques, with a view to identifying the most fit, the global optimum in the context of interest.