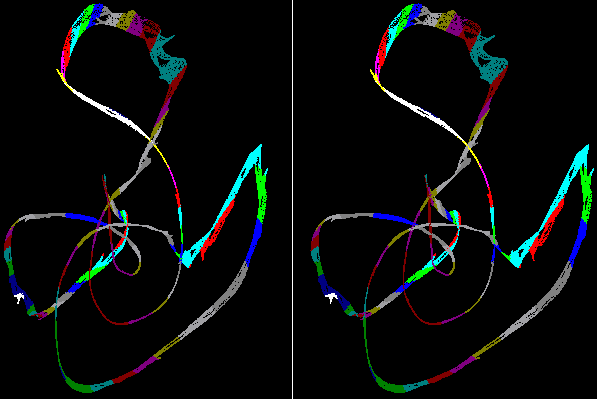
To view these images a similar technique is needed to that used to view Random Dot Stereograms. I find the easiest way to see these is to look slightly towards your nose until the two images merge in the background. With a little practice they will be locked together by the eye and come into focus. You will then see a true three dimensional image of the attractor. The fourth spatial dimension is colour coded into 16 bands so that all 4 dimensions are now visible from one 2 dimensional medium !
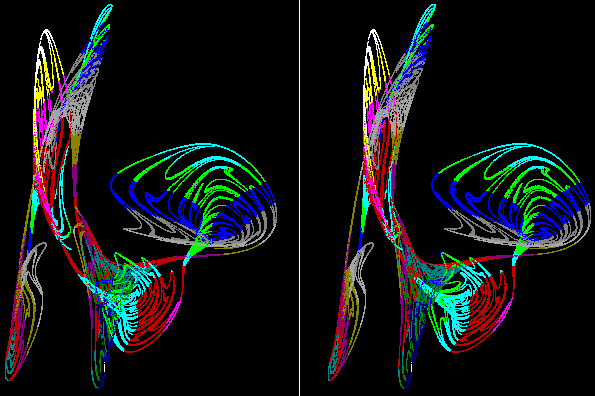
These images use time as the fifth dimension and integrate the trajectories over a long period. At any instantaneous time (as in a photograph) only a single point would be visible. The structure exists in a strange realm that we cannot easily see with our normal senses.
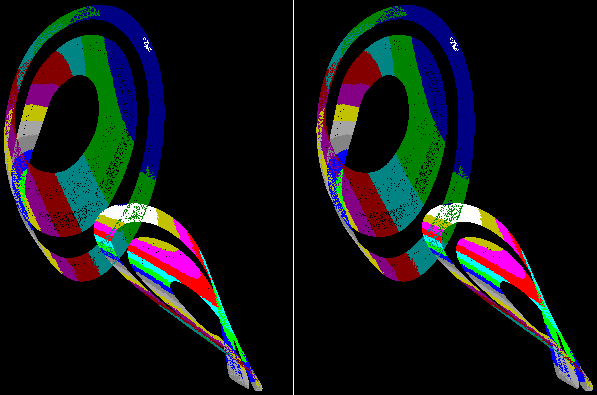
This image shows that attractor parts that are quite separate in 3 dimensions are nethertheless connected in the fourth dimension of space. A finding from Quantum theory (proved experimentally by Alain Aspect) is that all things are connected in some way outside the 3 dimensions of space and 1 of time with which we are familiar. Perhaps a 4th spatial dimension, as illustrated here is part of the reality we inhabit...
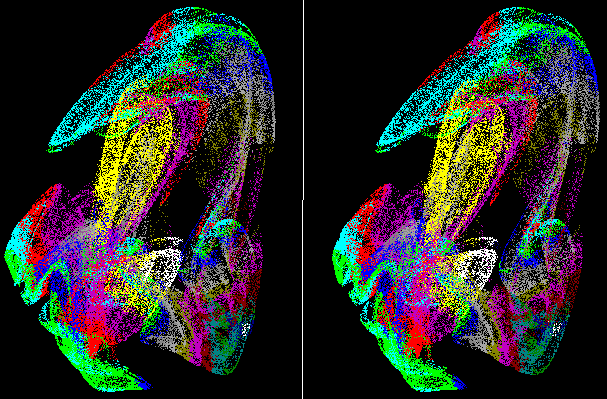
This image resembles a bird, the head and beak are visible with some indication of wings, it reminds one of an embryonic form. Could it be possible that there is a relationship between form in nature and attractors ? We already see the resemblance between natural forms and fractals, could the two concepts together explain how things grow and develop ? That possibility remains, although further work is necessary to clarify the concept.

The previous images have been discontinuous, the next point could be anywhere in the figure. Conventional science deals with continuous functions, Ordinary Differential Equations. Yet these too have attractors. The image above is one such, showing a complex path in phase space.
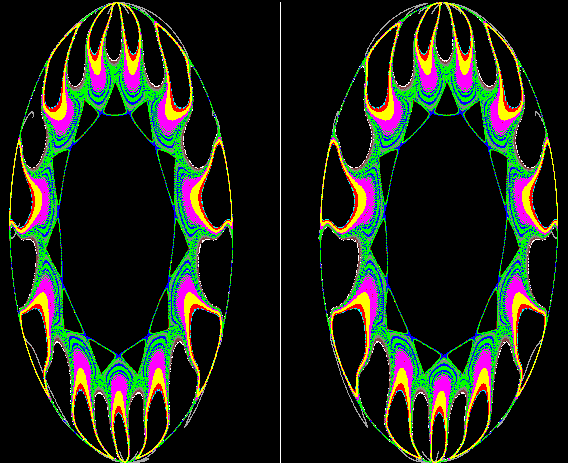
Many physical systems conserve certain quantities. The phase space for these Hamiltonian systems is also conserved, but attractors nethertheless exists, as this example shows.
An online book explaining strange attractors in detail and containing the software needed to generate these images can be obtained from: Sprott's Strange Attractors - Creating Patterns in Chaos